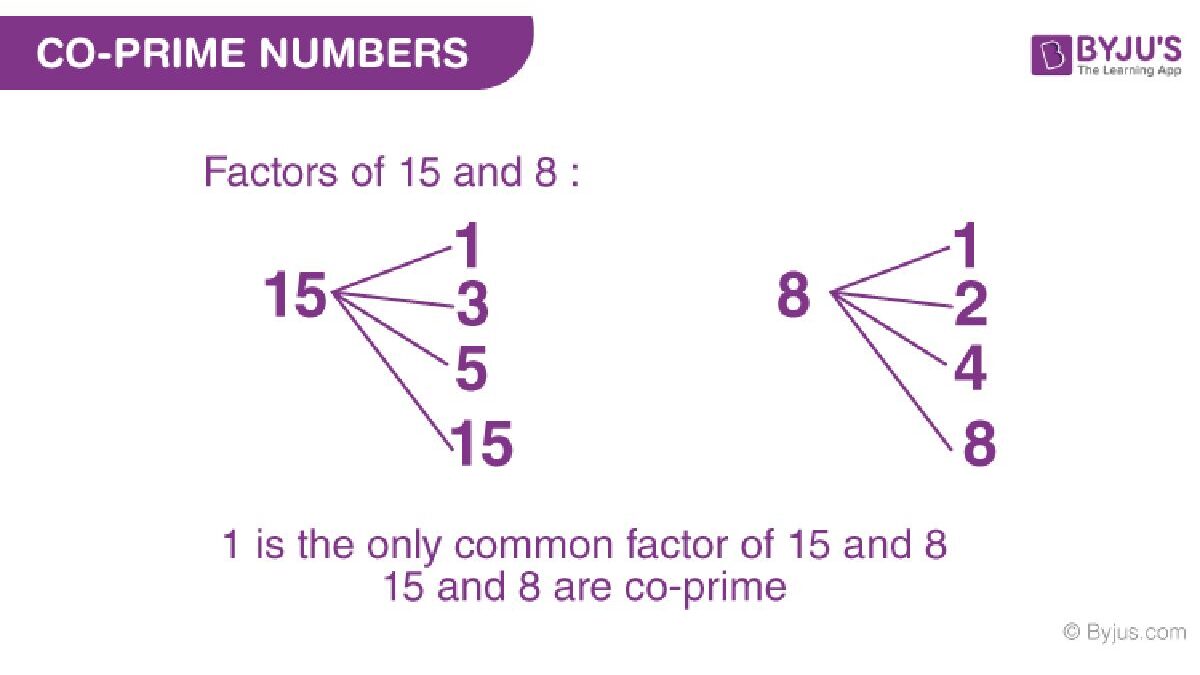
We all are aware of what a prime number is. So, what is a co-prime number? Math can be fascinating because we discover many interesting facts through it. Read on for more.
Co-prime numbers have no mutual factor other than 1. A set of co-prime numbers must contain at least two figures. For example, 4 and 7 have only 1 as their maximum common feature. Co-prime numbers are also shaped by two composite numbers, 4 and 9.
Table of Contents
What is a co-prime numbers?
Co-prime Numbers are a collection of integers or numbers that stake only the number 1 as a shared factor.
For instance, x and y are two positive numbers co-prime if and only if they have one common aspect, and thus HCF(x, y) = 1. In other words, co-prime numbers are a duo of numbers or integers with only one mutual factor, namely that their uppermost mutual factor (HCF) is 1. Co-prime numbers are also known as equally prime numbers or relatively prime numbers. It is serious to have two numbers to procedure co-primes.
How do I find co-prime numbers?
Think of a duo of numbers; if no positive integer other than one can divide them, the two are co-prime.
Illustration 1- 21 and 22
For figures 21 and 22-
| Figure | Features |
| 21 | 1, 3, 7 |
| 22 | 1, 2, 11 |
Now, 21 and 22 shares only one factor, that is 1. As an outcome, the HCF is 1, and they are co-prime.
Illustration 2- 21 and 27
For Figures 21 and 27-
| Figure | Features |
| 21 | 1, 3, 7 |
| 27 | 1, 3, 9 |
In this case, 21 and 27 dividends two features, 1 and 3. They had an HCF of 3 and are no co-prime.
Co-prime figures list
Co-prime numbers |
Pair of Co-prime number duos |
| 1 | (1,7), 8(1,8), 22(1, 22) |
| 2 | 3(2,3), 5(2,5), 7(2,7), 9(2, 9), 11(2, 11), 13(2,13), 15(2,15) |
| 3 | 4(3,4), 5(3,5), 7(3,7), 10(3, 10), 11(3, 11), 15(3, 15), 22(3, 22) |
| 4 | 5(4,5), 7(4,7), 9(4,9), 11(4, 11), 13(4, 13), (154, 15), 17(4, 17) |
| 5 | 6(5,6), 7(5 7), 8(5,8), 9(5,9), 11(5, 11), 12(5, 12), 14(5, 14) |
Properties
Co-prime numbers have six properties.
The universal co-prime number is One. You can combine one with any numeral, and they will be co-prime. For instance, (1,2), (1,3), (1,8), (1,15), (1,532), (1,2568).
In a number order, the integer instantly following and preceding a number is co-prime. For example, the number 33; thus, the number following 33 will be 34, which is co-prime to 33. Therefore, the number before 33 is 32; 33 is a co-prime.
Because 0 is a factor-less number, it is not co-prime with any other numeral.
Even numbers can not ever be co-prime because they all are part of a common factor other than 1, which is 2.
If we multiply two co-prime numbers, the resulting numbers are also co-prime. For illustration, 3+4 = 7, and 3 x 4 = 12, the outcomes 7 and 12 have only one mutual factor; thus, they are co-prime.
An odd number and an even number are also co-prime. However, if the figures have 0 and 5 at the ones or unit places, they are not co-prime because they have an HCF = 5.
Prime numbers are co-prime numbers. For sample, (11,13); 11=1×11 & 13= 1×13
Co-prime and twin prime numbers
The set of two numbers with precisely one composite number is known as twin prime numbers.
Co-prime numbers have an HCF of one. Matching prime numbers, on the other hand, are prime numbers with a change of two. For example, 7 and 5 are twin prime numbers. The following points distinguish co-prime and twin-prime numbers.
Co-prime number |
Twin prime number |
| The difference between two primes will be any whole number. | The difference between two twin primes is always two. |
| Co-prime numbers can be either prime numbers or composite numbers. | Twin prime numbers are always prime numbers. |
| Co-prime numbers can be twin prime numbers or not. | All twin prime number sets are co-prime. |
| Any number can join 1 to form a co-prime pair. | 1 form a twin prime duo only with 3. For cases 1 and 3 as (3-1=2) |
Co-prime numbers from 1 to 100
There are several pairs of primes reaching from 1 to 100. Among them are-
- 13 and 14
- 28 and 57
- 1 and 99
- 2 and 97
- 46 and 67
- (75 and 41)
Therefore, any number with a mixture of 1 can be written as a co-prime pair, Like (22,1), (31,1), (4,1), (90,1), (1,100). Numerous co-prime numbers from 1 to 100 are defined in this manner.
Key takeaways
The co-prime numbers do not have to be a prime number. It is also known as a composite number.
Any two prime numbers given must be a Co-prime.
Sets of two even numbers can never be co-prime.
Any number can form a co-prime pair with 1 (one).
Any two consecutive numbers are indeed co-prime.
Two even numbers can never be co-prime.
Co-prime numbers need not be prime numbers. For instance, 12 and 35 are co-prime numbers. Therefore, 12 and 35 are not prime numbers.
FAQs
Q1. What is the coprime of 60?
Answer- For instance, 60 is divided by two to profit 30, divided by two to yield 15, and divided by three to profit five (another prime). Hence, 60 = 2 × 2 × 3 × 5.
Q2. What is the smallest co-prime number?
Answer- 2 is the smallest prime number. A number must have only two aspects- 1 and the number itself to be prime.
Q3. How do you check if two numbers are co-prime?
Answer- If the greatest common divisor of two numbers, X and Y, is 1, they are said to be Co-prime or mutually prime.